こんにちは、おぐしです。
順番を決めるときや、役割分担を決めるときなど、簡単に、かつ公平に決める方法として採用されている「じゃんけん」。
じゃんけんのルーツは中国であるものの、じゃんけん自体は日本でブラッシュアップされてできたものだそうです。
今では全世界に広がって、その上定着しているというのだから凄いですよね!
さて今回は、じゃんけんではなく、その派生である「ゲーマーじゃんけん」のお話です。
ゲーマーじゃんけんとは
「ゲーマーじゃんけんって何?」と、気になった人もいることでしょう。
僕も、ボードゲーム会に参加したときに、初めてゲーマーじゃんけんの存在を知りました。
スタートプレイヤーを決めたい時、特に人数が多い場合、普通にじゃんけんすると時間がかかってしまいますよね。
人数が多ければ多いほど、じゃんけんだとあいこが続いてしまう、誰もがそんな経験をしたことがあるのではないでしょうか。
そこで、サクッと短時間で決まるように考えられた方法が「ゲーマーじゃんけん」です。
ゲーマーじゃんけんの流れ
「少ない手が勝ち」、もし手の数が同じなら「手が強い方の勝ち」の条件で勝敗を決めるのが、ゲーマーじゃんけんです。
流れを分解すると、以下のようになります。
パターン表
| グー 人数 | チョキ 人数 | パー 人数 | 判定 |
|---|---|---|---|
| ✊1人 | ✌2人 | ✋3人 | ✊1人の勝利。 |
| ✊1人 | ✌1人 | ✋3人 | ✊1人の勝利。 |
| ✊3人 | ✌5人 | ✋5人 | ✊3人の勝利。 再度✊3人でゲーマーじゃんけん。 |
| ✊3人 | ✌5人 | ✋3人 | ✋3人の勝利。 再度✋3人でゲーマーじゃんけん。 |
| ✊3人 | ✌3人 | ✋3人 | あいこ。 |
| ✊1人 | ✌1人 | ー | ✊1人の勝利。 |
| ✊3人 | ✌1人 | ー | ✌1人の勝利。 ※じゃんけんではないので少ない方の勝ち。 |
| ✊3人 | ✌3人 | ー | ✊3人の勝利。 再度✊3人でゲーマーじゃんけん。 |
| ✊5人 | ✌3人 | ー | ✌3人の勝利。 ※じゃんけんではないので少ない方の勝ち。 再度✌3人でゲーマーじゃんけん。 |
| ✊3人 | ー | ー | あいこ。 |
ゲーマーじゃんけんでは数倍も早くスタPが決まる!
ノーマルなじゃんけんとゲーマーじゃんけんでは、実際にどれだけ変わるのでしょうか。
以下は、1回で勝者が決まる場合の確率を算出し、人数別にグラフにしたものです。
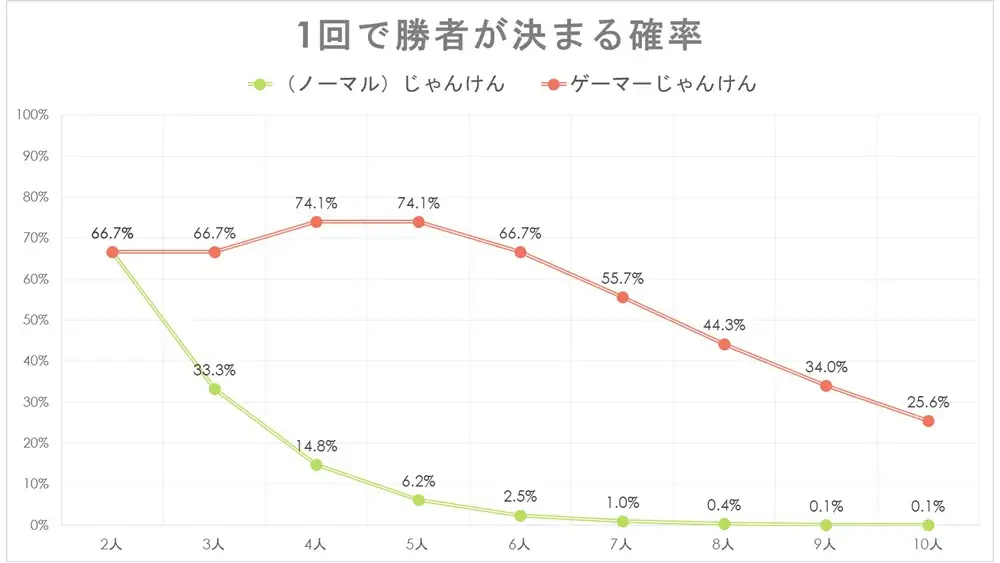
ゲーマーじゃんけんでは、3人でも66.7%で十分高い確率ですが、4〜5人の場合に74.1%と、一番高い確率になっています。
グラフで見ると、「ゲーマーじゃんけんの方が倍以上早く決着がつく」ことが一目瞭然ですね。
確率の計算式を紐解いてみる
ここで、(ノーマル)じゃんけんとゲーマーじゃんけんの確率を計算する式をみてみましょう。

僕もまとめながら数字アレルギーが出ました…
計算を簡易的にするため、「1回で勝者が決まる確率」としました。
「条件:1回で勝者が決まる確率」
(ノーマル)じゃんけんの確率計算
割とシンプルに、確率計算できます。
1回で勝者が決まるということは、2種類の手しか出されない場合のみです。
手の出し方は、1人が✊なら他者が✌(✋は0人)、1人が✌なら他者が✋(✊は0人)、1人が✋なら他者が✊(✌は0人)、この3パターンのみ。
最低2人から成立しますね。以降、変数Nを人数とします。
これらの条件より、内訳と人数の条件は以下のように定義できます。
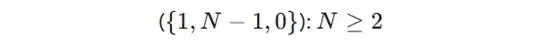
N人であれば、”3×N“パターンの組み合わせがあると計算されます。
そして、全員の手の組み合わせが”3N“通り。よって、確率の式は以下のようになります。
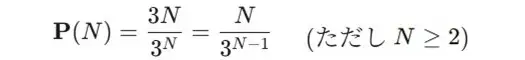
ゲーマーじゃんけんの確率計算
ゲーマーじゃんけんの勝敗のルールは2つのステップからなります。
ひとつは「少ない手が勝ち」。手の数が同じなら「手が強い方の勝ち」です。
ゲーマーじゃんけんのルールで、1回で決着がつくパターンは3つあります。
- パターン1:1人がある手で、他者が1人目と異なる1種類の手。
- パターン2:2種類の手を1人ずつ、他の1種類の手を2人以上。
- パターン3:1人がある手で、他の2種類の手が2人以上ずつ。
・パターン1:1人がある手で、他者が1人目と異なる1種類の手。
通常のじゃんけんと同じで、2種類の手であるケースですね。
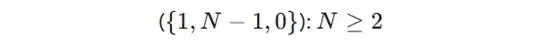
2人の場合は(ノーマル)じゃんけんと同じルールになりますが、3人以上の場合は、同じ手の少ない方が勝者になります。
つまり、人数(N)が2人と3人以上とで、計算式が変わります。
2人の場合は、(ノーマル)じゃんけんと同じ計算式になり、確率は2/3です。
3人以上の場合、手の出し方は、1人が✊なら他者が✌or✋、1人が✌なら他者が✋or✊、1人が✋なら他者が✊or✌の6パターン。
N人であれば、決着パターンは”6N“あり、全員の手の組み合わせが”3N“通りなので、以下の計算式で表現できます。
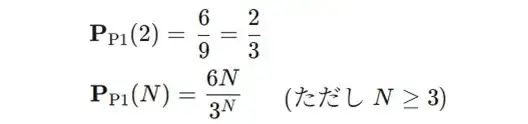
・パターン2:2種類の手を1人ずつ、他の1種類の手を2人以上。
3種類の手が出た場合に、1回で勝敗が決まるのは、1種類の手を1人、もう1種類の手を1人、残る1種を2人以上出した場合です。
この条件は、4人以上でなければならず、内訳と人数の条件は以下になります。
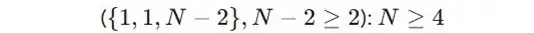
「2種類の手を1人ずつ」出すパターンは、✊✌、✌✋、✋✊の3通りです。
1種類目を1人、2種類目を1人で、人の組み合わせは”N×(N-1)”となり、3通りあるので、勝ちパターンは”3N(N-1)”です。
全員の手の組み合わせが”3N“通りなので、以下の計算式で確率が表現できます。
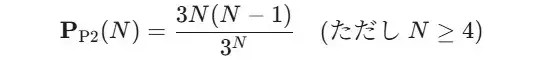
・パターン3:1人がある手で、他の2種類の手が2人以上ずつ。
3種類の手が出た場合のもうひとつのパターンが、1種類の手が1人で、残り2種類が2人以上出す場合です。
5人以上でなければ成立しないので、内訳と人数の条件は以下のようになりますね。
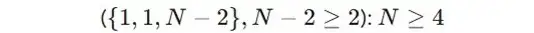
1人は、✊✌✋の3種類を出すパターンがあり、N人いる場合は、”3N“通りの出し方があります。
他の人(N-1)は、1人目が出した以外の手2種類から選ぶので、”2N-1“通り。
そのうち、いずれかの手が0人(1パターン)と、1人(N-1パターン)である場合を除くので、”{1+(N-1)}×2=2N“を差し引かいて、”2N-1-2N“となります。
全員の手の組み合わせが”3N“通りなので、確率は以下のようになります。
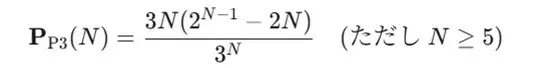
3つのパターンを合算する
これで、全てのパターンが揃いました。
あとは、3パターンの式を合算すればOKです。
それぞれのパターンで条件が変わるため、厳密には4人までは正しく算出できませんが、おおよそ以下の式で、ゲーマーじゃんけんの確率が導き出せます。
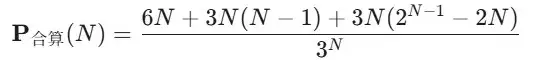
さて、、、確率の式を導きましたが、もしあなたがここまでの解説を「ふむふむ」と読み解いたのであれば、とても論理的な思考の持ち主なはず。
そんなあなたには、テンプルコードをおススメします!
『テンプルコード』は、論理思考と駆け引きを楽しめる1〜4人用の推理系ボードゲームです。
自分だけが知らない「3つの印の並び順」を、共通のカードを使って推理し、誰よりも早く正解を導くことを目指します。
ゲーマーじゃんけんをWebアプリ化
ゲーマーじゃんけんのルールを覚られるよう、ゲーマーじゃんけんアプリを作成しました。
何度か遊べば、すぐにルールをマスターできるでしょう!
あなたも、ゲーマーじゃんけんを覚えて、みんなと使ってみてはいかがでしょうか?
それでは、サクッと楽しいボドゲライフを!



